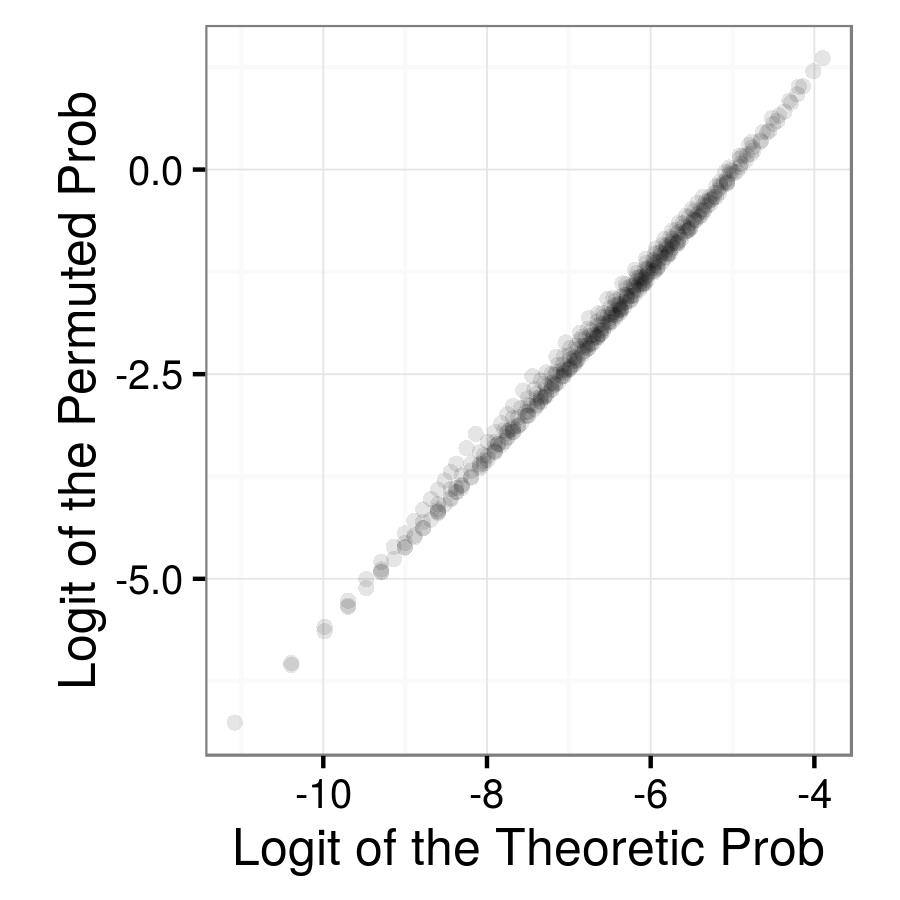
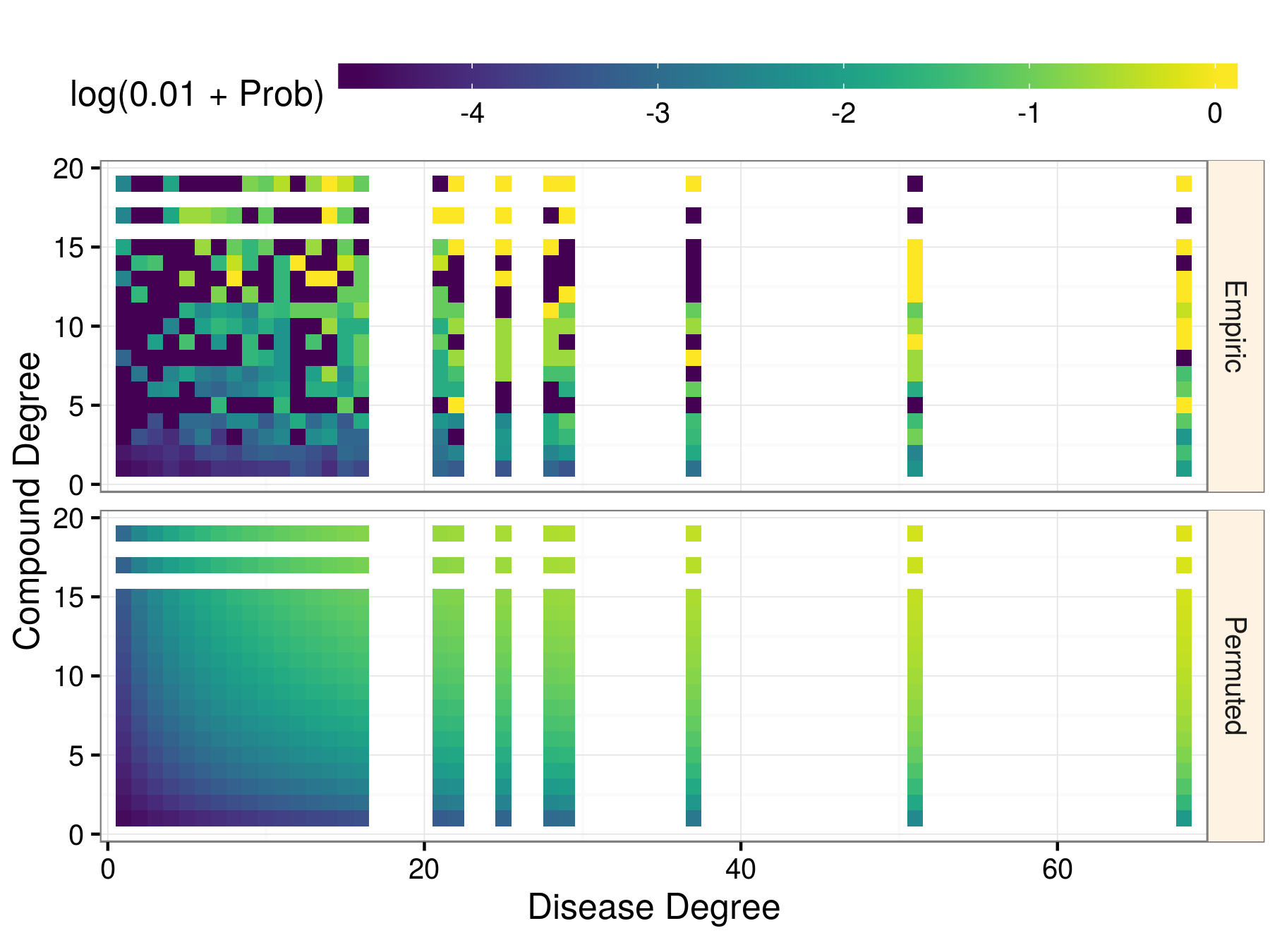
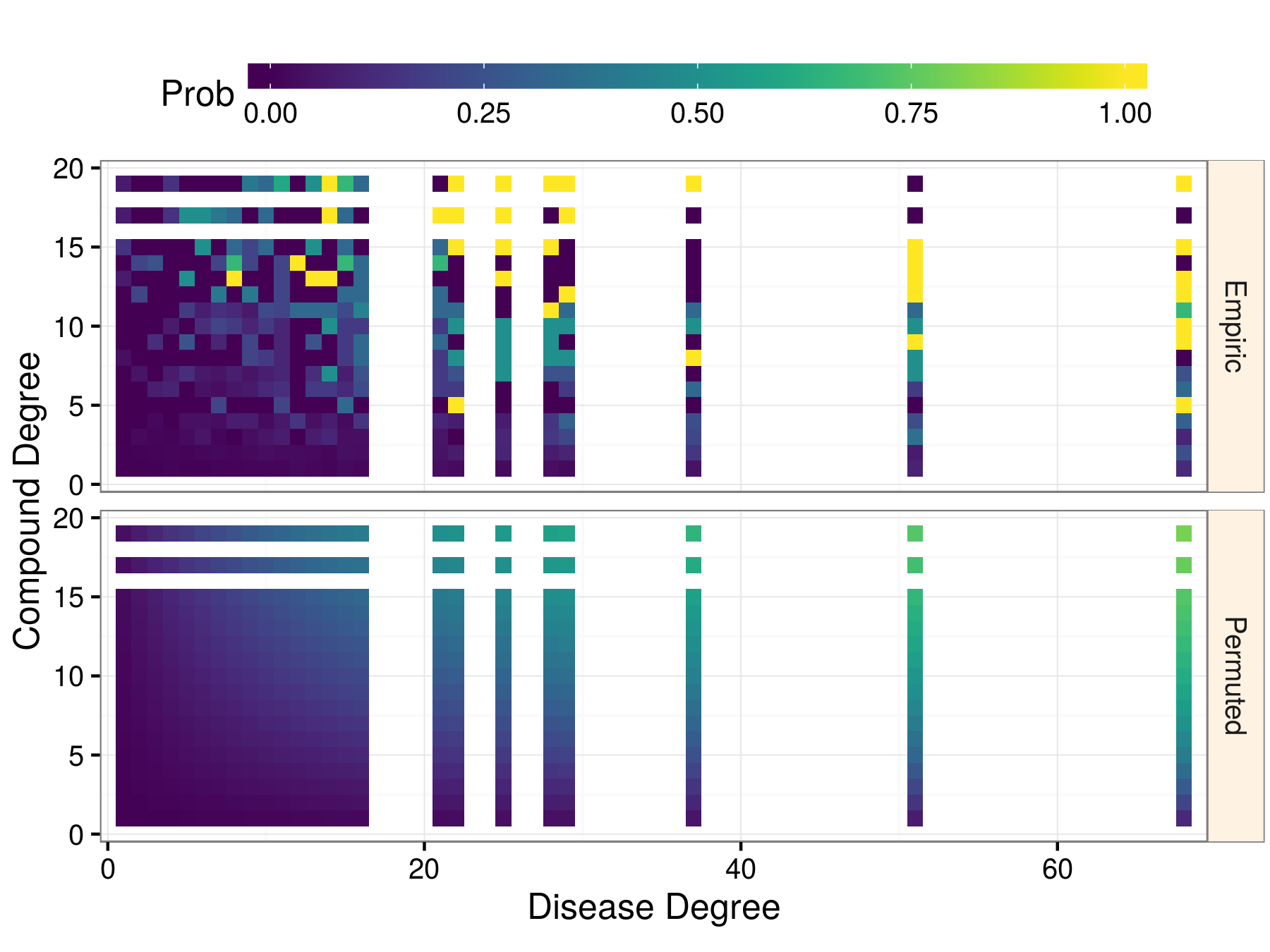
|
|
|
Status:
In Progress
Views
79
Topics
Referenced by
Cite this as
Antoine Lizee, Daniel Himmelstein (2016) Network Edge Prediction: Estimating the prior. Thinklab. doi:10.15363/thinklab.d201
License
Share
|